• Business Problem
• Touchpoints & Surveys
• Problem formulation
• Solving the problem with Probabilistic Programming
• Experiment
  • Generate data
• Results
  • 1. Model the attribution from touchpoints
  • 2. Model the attribution from Surveys
  • 3. Integrate both spending and surveys
  • 4. Model the touchpoint measurements from a hypothetical spending
• Final Thought
• Citation
• Appendix
  • A. packages
  • B. Generate Data
  • C. Object-oriented construction
  • D. Modeling attribution from touchpoints
  • E. infer the subscription per channels from the surveys
  • F. Integrate both spending and surveys
  • G. Model the touchpoints measurement from hypothetical spending

Business Problem

This blog is part of a series on marketing mixed model. In my last blog post, I explored Bayesian inference as an option for estimating the advertising lag and saturation effect. In this blog post, I will tackle a different problem, namely, how to assign credits to marketing channels. This problem is called Attribution. This problem is important if the marketers want to know which marketing channels are effective and which ones are not.

Touchpoints & Surveys

The heart of the matter is really about comparing effectiveness of different marketing channels. To operationalize on this high-level problem, we can ask:

for all the customers in a given period, how many come from this marketing channel, etc.

The most straight-forward way to determine credit is to do a controlled experiment, where we can precisely assign who get exposed to a specific advertising channel. I have dealt with the experiment data in my old blog post here. However, experiments are costly, so it’s not often feasible to do for all channels.

Nowadays in the world of digital products, there are many ways to measure users interactions. There are digital sensors such as clicks and views keeping tracks of customer interactions with the products, aka. “land on the websites”. These are known as touchpoint.Some marketing channels such as online ads or emails are naturally well-integrated with the digital touchpoints.

We can also ask the customers directly how they come into contact with the products. These are surveys. Some channels such as TV commercials podcasts or word-of-mouth rely more on survey data. Using the term “survey” in a broader sense, one can think of coupon codes as something similar in the sense that a portion of customers using coupon codes will is a measurement of how many people might come into contact with the advertising channels with those coupon codes.

Problem formulation

The problems we are facing here is how to create a joint models that take all information into accounts and assign credits to each channels.

What we need to keep in mind is that in reality there is no ground truth on which the model can be trained. We never know the true assigned credits for each channel. We only know the total number of customers aggregated from all channels. In other words, our problem is not going to be a supervised learning in the machine learning sense. The problem requires inferring hidden variables from observations. In this case, the assigned credits are hidden variables.

Solving the problem with Probabilistic Programming

In my previous two blogs first Pymc3 and [second Pyro]https://vincentk1991.github.io/adstock-pyro/), I gave an overviews and sample codes for the probabilistic programming packages in Python. In this blog I used NumPyro. Numpyro is a new probabilistic programming package in Python that enables linear algebra-specific JIT (Just-In-Time) compilation. The results is a big speed improvement (more than 100x faster).

NumPyro uses NumPy backend, unlike Pymc3 which uses Theano or Pyro which uses Pytorch. I found NumPyro to be very similar in style to Pyro with a minor exception where Pytorch and NumPy uses different commands. For example, Pytroch may uses torch.mean(x, axis=1) while NumPy uses np.mean(x,dim=1). Other commands dealing with probability distributions are basically shared with Pyro. For example, both numpyro.sample('name',dist.Normal(0,1)) and pyro.sample('name',dist.Normal(0,1)) are used to return random sample from a Normal distribution with means = 0 and standard deviation = 1. The bottom line is that the learning curve is low.

The speed improvement is the main reason why I want to use NumPyro. The attribution model can be really quite complex. It would take hours to run Markov Chain Monte Carlo on the attribution model In Pymc3 or Pyro. The same model may take just a few seconds in NumPyro, meaning we will have more time trying different priors, optimizing the model for accurary, or exploring features of the model.

Experiment

The code for this work is included in the appendix.

Generate data

The codes for this part is included in the appendix section B.

I created a synthetic dataset consists of 6 months data with 5 channels. The features in the dataset are spending (a hypothetical unit such as 100K$ or 1M$), touchpoint measurement (this could be views, clicks, landing, etc.), monthly subscription, and monthly surveys. The spending has a diminishing return on the touchpoints. The diminishing returns is assumed to have a log shape. There are many functions that can be used to create diminishing returns effect but the log function is easy and parameter-free. To avoid the negative result, we add 1 element-wise to all inputs before taking log.

The subscription is a binomial process of the touchpoint counts. That is to say, every person who comes into contact with the products through this touchpoint has a probability X to buy the product. Each channel is associated with one touchpoint for the sake of simplicity. In reality one channel can have many touchpoints and some may not have any touchpoints.

Note here that the monthly subscription of each channel is the ground truth of this synthetic data. In real world daata this is unknown. The attribution model will not use this information, but only need the aggregated monthly subscription which is available in the real world. However, we will need the ground truth to see how well the model is working.

The survey is a binomial process of the subscription counts. That is to say, for every person who subscribe has some probability p of answering the surveys.

Results

In this section, I will explore different attribution modeling strategy. You can go to the appendix at the end to see all the codes. But first, if you do not have NumPyro, you’d need to

pip install numpyro==0.2.4

First in the appendix section C, I created the NumPyroAttribution parent class that will be used throughout the work. The base class initializes data as class attributes. The base class has run method which will run our MCMC sampling. It also has predict method which I will use for predictng the out-of-sample data. The model method is not implemented and will be implemented in children classes. The result is stored as MCMC traces and can be retrieved using get_traces method. These traces will be used subsequently to find distribution, means, and credible intervals.

1. Model the attribution from touchpoints

The code for this section is included in the appendix section D.

I created the NumPyroTouchInference child class which inherits from the parent class. The child class implements the model.

In this first model, I’m interested in the probability of subscription given the users comes into contact with the touchpoint. The prior distribution is a uniform distribution from 0 to 1, representing the probability of subscribing given contacting the touchpoints. I use Bayesian regression to regress the subscription per channel given the probability of subscription for each channel given the touchpoints and numbers of each touchpoint.

The result is shown in figure 2.

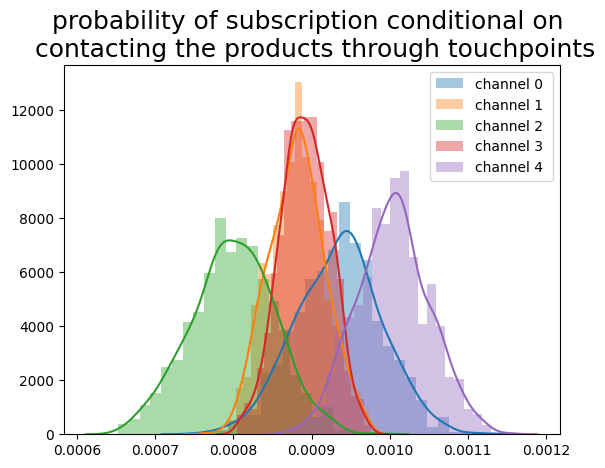
Figure 1. Bayesian inference of the subscription probability given contacting the touchpoint.

The subscriptions per channel are hidden variables. However, I know that they must sum to the total number of subscription in a given month. So I include the sum condition as a constriant.

In the plot below, I plot the attributed subscription per channel against the ground truth. The data are arranged from month 0 to 5 and from channel 0 to 4. The average subscription per channel is shown as a dash line. The ground truths are marked as X. The 90% credible intervals are shown as lines.

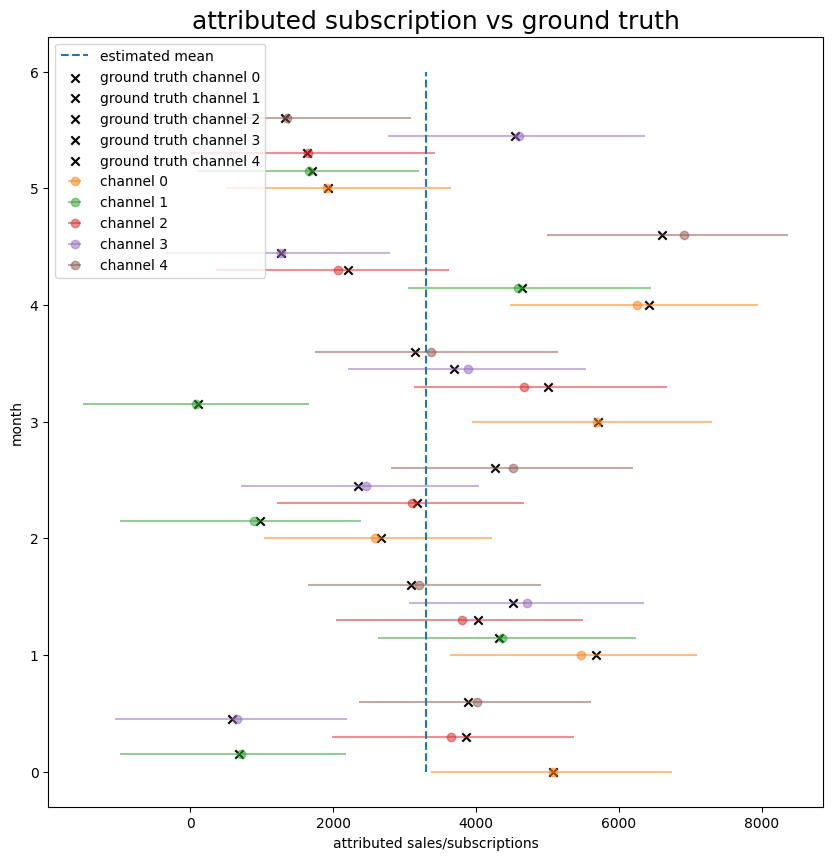
Figure 2. Bayesian inference of the attribution given the touchpoint data.

First thing to note is how wide the credible intervals are. My thought is that this is perhaps due to the unconstrained priors that I use. In the real world, choosing the appropriate prior is where the domain expertise comes into play. The practitioners will have a rough idea about what the priors look like because they may have an idea how well the marketing channels are performing. They can choose to incorporate their ideas to the model by adjusting the priors. This should hopefully gives a model much better constraint.

2. Model the attribution from Surveys

In this section, I try to work out how I can use survey data to construct an attribution model. The code on this section is shown in the appendix E.

The modeling strategy that I used is to infer the subscription from the surveys. This is the Bayesian regression where the coefficient is the average number of attribution per 1 survey answered. This is one over probability of answering the survey.

Similar to the model in the previous section, we can plot the result against the ground truth.

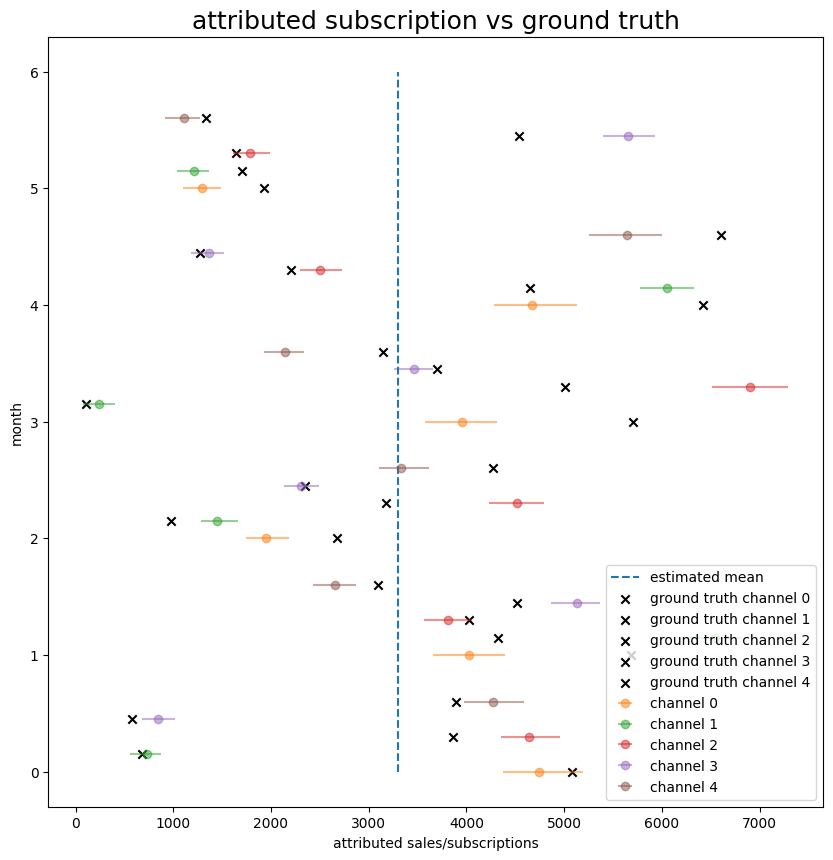
Figure 3. Bayesian inference of the attribution given the survey data.

3. Integrate both spending and surveys

In this section I try to simulate a scenario where I have 5 channels. 3 channels only have touchpoint data, and 2 channel only have survey data. The code for this section is in the appendix F.

The strategy that I use is to fit the two Bayesian regression separately but concatenate the result to make the aggregated subscription. The aggregate is constrained by the overall monthly subscription.

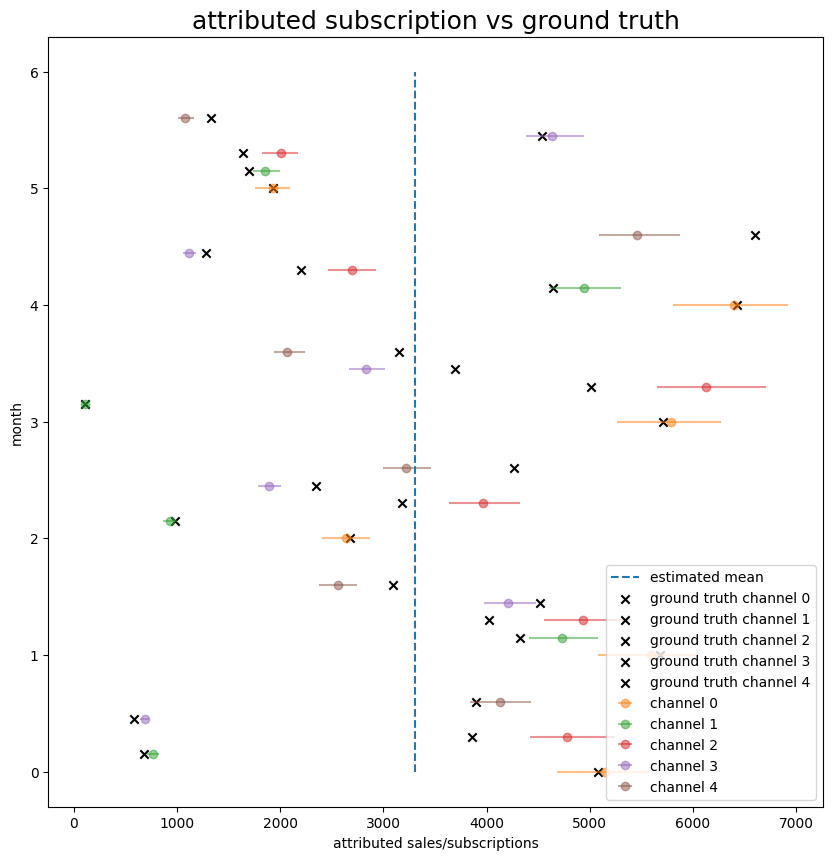
Figure 4. Bayesian inference of the attribution given either touchtpoint data or survey data.

4. Model the touchpoint measurements from a hypothetical spending

The purpose of doing the attribution model is that we then can create a hypothetical spending strategy and inject it to the trained model to see how well our spending generate subscription. In this model, I will first train the model on the spending and touchpoints, then using the predict method, I can sample the posterior predictive distribution from the out-of-sample data.

The training phase is similar to the section 1. The out-of-sample data consists of 3 month spending data on 5 channels. The posterior distribution that I get is the predicted touchpoints measurement.

I plot the result which is the predicted touchpoint measurement given the spending as a distribution against the ground truth (shown as dash lines).

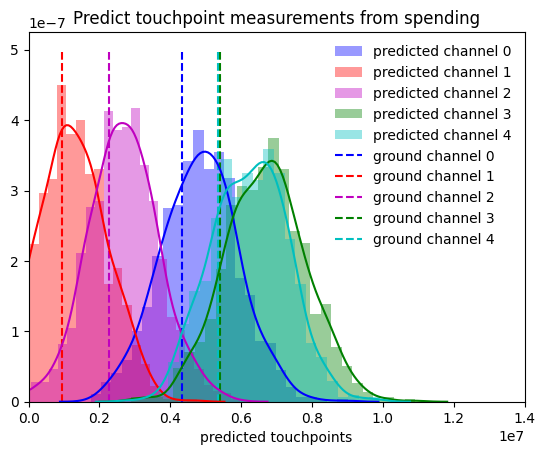
Figure 5. Bayesian inference of the touchpoint measurements given a hypothetical spending data

Final Thought

I hope that this blog post give a rough idea about how one can implement Bayesian inference in Python to tackle the attribution problem. While working on this blog, I realized how much more complex is real attribution problem really is.

Choosing the appropriate priors is crucial especially when the model is getting complicated, the effect of priors can be strong. In my example, I give every channel the same priors, so while it may fit one channel perfectly, it does not work well for other channels. Tuning the priors to be realistic is where I think domain expertise will shine.

A more realistic attribution model should be a time series. This would include regressing on the dummy variables representing the trends and seasonality. The spending can have lag and carryover effects, so the adstock function has to be incorporated. The touchpoints can have daily resolution while the surveys have monthly resolution. So we need to choose the appropriate granularity of the data.

I haven’t implemented a scenario where one channel receive more than one touchpoints or more than one surveys. How do all measurements relate to one another and to the subscriptions has to be worked out. As important is how the experiment result is incorporated into the model.

Finally, what should we do with channel interactions? One can imagine that marketing advertising can have synergistic effects where both at the same time are better than sum of the parts.

And unfortunately I will not be able to address all of these fun problem a single blog post. So perhaps I will have time to revisit this problem again.

Citation

• NumPyro This is the main NumPyro website that keep the documentation and a few example codes.

Appendix

A. packages

import jax.numpy as np
from jax import random, vmap
from jax.scipy.special import logsumexp
import matplotlib.pyplot as plt
import numpy as onp
import pandas as pd
import seaborn as sns
!pip install numpyro==0.2.4

import os
import numpyro
from numpyro.diagnostics import hpdi
from numpyro.infer import Predictive
import numpyro.distributions as dist
from numpyro import handlers
from numpyro.infer import MCMC, NUTS

plt.style.use('bmh')
if "NUMPYRO_SPHINXBUILD" in os.environ:
    print('set svg')
    set_matplotlib_formats('svg')

assert numpyro.__version__.startswith('0.2.4')

B. Generate Data

Below is the codes for generating the data. I set the function such that for every log unit of spending, we get 10 millions landing on touchpoints. For every landing there is 0.0009 probability of subscription. For every subscription, there is 0.01 probability of answering the survey.

def generate_n_channel(sample_size,num_channel,spending = 0.1,touch_multiplier = 1e7,sub=0.0009,survey=0.01,diminishing_return=True, numpyro = False):
  
  '''
    generate data for attribution model
   input:
     sample_size = number of months data is available
     num_channel = number of channels consider
     touch_multiplier = coefficient of spending on touchpoints
     sub = probability of people who come into contact with the touchpoints to subscribe/buy the product
     survey = probability of customers/subscribers to answer the survey
     diminishing_return = whether the effect of spending is linear or non-linear (apply log transformation)
     numpyro = whether to return the output as pytorch array or numpy array
     
   output:
    a batch of
      1. spending array
      2. touchpoint array
      3. subscription array
      4. survey array
      5. aggregated subscription array
  '''
  
  def semilog(array,beta,alpha = 0):
    return alpha + beta*onp.log1p(array)

  spending_arr = onp.abs(onp.random.normal(1,1,size=(sample_size,num_channel)))
  if diminishing_return:
    touch_arr = semilog(spending_arr,touch_multiplier)
  else:
    touch_arr = spending_arr * touch_multiplier

  touch_arr = onp.round(touch_arr).astype(int)
  sub_arr = onp.random.binomial(touch_arr,p=sub)
  survey_arr = onp.random.binomial(sub_arr,p=survey)
  sum_sub = onp.sum(sub_arr,axis=1)
  if numpyro:
    return np.array(spending_arr), np.array(touch_arr), np.array(sub_arr),np.array(survey_arr), np.array(sum_sub)

  else:
    return torch.tensor(spending_arr), torch.tensor(touch_arr).type(torch.float64), torch.tensor(sub_arr).type(torch.float64),torch.tensor(survey_arr).type(torch.float64), torch.tensor(sum_sub).type(torch.float64)

C. Object-oriented construction

Here below is the base class construction that we will need. The class contains methods for running MCMC and predicting posteriors. Note that the standardize method is yet to be implemented.

rng_key = random.PRNGKey(0)
rng_key, rng_key_ = random.split(rng_key) # The random number keys
class NumPyroAttribution(object):
  def __init__(self,spend_data,subscription_data,touch_data = None,survey_data=None):
    self.spending = spend_data
    self.subscription = subscription_data
    self.survey = survey_data
    self.touch = touch_data
    self.sample_size = spend_data.shape[0]
    self.num_channel = spend_data.shape[1]
    self.num_survey = None
    self.num_touch = None
    if self.survey != None:
      self.num_survey = self.survey.shape[1]
    if self.touch != None:
      self.num_touch = self.touch.shape[1]
    self.traces = None
    self.predict_traces = None

    self.predict_spending = None
    self.predict_subscription = None
    self.predict_survey = None
    self.predict_touch = None
    self.predict_sample_size = None
    self.predict_num_channel = None
    self.predict_num_survey = None
    self.predict_num_touch = None
    
  # add the out-of-sample data
  def add_predict_data(self,predict_spend=None,predict_subscription=None,predict_touch=None,predict_survey=None):
    self.predict_spending = predict_spend
    self.predict_subscription = predict_subscription
    self.predict_touch = predict_touch
    self.predict_survey = predict_survey
    self.predict_sample_size = self.predict_spending.shape[0]
    self.predict_num_channel = self.predict_spending.shape[1]
    if self.predict_survey != None:
      self.predict_num_survey = self.predict_survey.shape[1]
    if self.predict_touch != None:
      self.predict_num_touch = self.predict_touch.shape[1]

  # run MCMC on the sample data
  def run(self,num_warmup=200, num_samples=1000):
    kernel_attribution = NUTS(self.model)
    mcmc_attribution = MCMC(kernel_attribution, num_warmup, num_samples)
    mcmc_attribution.run(rng_key_)
    self.traces = mcmc_attribution.get_samples()

  # call the posterior predictive sampling
  def predict(self):
    if self.traces == None:
      print('MCMC has not been run')
      return
    predictive = Predictive(self.model,self.traces)
    self.predict_traces = predictive(rng_key_,predict=True)
    return self.predict_traces

  # not implemented
  def model(self,predict=False):
    pass
   
  # return the MCMC traces
  def get_traces(self):
    if self.traces == None:
      print('MCMC has not been run')
    else:
      return self.traces

  
  def get_data_size(self):
    print('{} sample sizes, {} channels, of {} touch points, {} of surveys'.format(self.sample_size,self.num_channel,self.num_touch,self.num_survey))

D. Modeling attribution from touchpoints

class NumPyroTouchInference(NumPyroAttribution):
  def __init__(self,spend_data,subscription_data,touch_data,survey_data):
    super(NumPyroTouchInference,self).__init__(spend_data,subscription_data,touch_data,survey_data)

  # the argument choose whether to perform MCMC inference from the sample data 
  # or prediction from the out-of-sample data
  def model(self,predict=False):

    if predict:
      spend_data = self.predict_spending
      subscription = self.predict_subscription
      num_channel = self.predict_num_channel
      num_touch = self.predict_num_touch
      num_survey = self.predict_num_survey
      touch_data = self.predict_touch
      survey_data = self.predict_survey
      sample_size = self.predict_sample_size

    else:
      spend_data = self.spending
      subscription = self.subscription
      num_channel = self.num_channel
      num_touch = self.num_touch
      num_survey = self.num_survey
      touch_data = self.touch
      survey_data = self.survey
      sample_size = self.sample_size


    sub_touch_coeff = numpyro.sample('sub_touch_ecoeff',dist.Uniform(np.zeros(num_channel),np.ones(num_channel)))

    # the numpyro.plate('name',shape) with the with context define the context 
    # in whch the model broadcast the repeaing observations (i.e. different months)
    with numpyro.plate('plate1',sample_size):
      per_channel_sub = sub_touch_coeff * touch_data
      
    numpyro.sample('channel',dist.Normal(per_channel_sub,1e3*np.ones_like(per_channel_sub)))
    mean_agg_sub = np.sum(per_channel_sub,axis=1)
    constraint = numpyro.sample('aggregate',dist.Normal(mean_agg_sub,1e2*np.ones_like(mean_agg_sub)),obs = subscription)

E. infer the subscription per channels from the surveys

class NumPyroSurveyBackwardInference(NumPyroAttribution):
  def __init__(self,spend_data,subscription_data,touch_data,survey_data):
    super(NumPyroSurveyBackwardInference,self).__init__(spend_data,subscription_data,touch_data,survey_data)
  
  def model(self,predict=False):

    if predict:
      spend_data = self.predict_spending
      subscription = self.predict_subscription
      num_channel = self.predict_num_channel
      num_touch = self.predict_num_touch
      num_survey = self.predict_num_survey
      touch_data = self.predict_touch
      survey_data = self.predict_survey
      sample_size = self.predict_sample_size

    else:
      spend_data = self.spending
      subscription = self.subscription
      num_channel = self.num_channel
      num_touch = self.num_touch
      num_survey = self.num_survey
      touch_data = self.touch
      survey_data = self.survey
      sample_size = self.sample_size

    sub_survey_coeff = numpyro.sample('sub_survey_coeff',dist.Normal(1e1*np.ones(num_channel),1e1*np.ones(num_channel)))

    with numpyro.plate('plate1',sample_size):
      per_channel_sub = sub_survey_coeff*survey_data
      
    channel_sample = numpyro.sample('channel',dist.Normal(per_channel_sub,1e2*np.ones_like(per_channel_sub)))

    # sum the subscription across channel to get monthly aggregate
    mean_agg_sub = np.sum(per_channel_sub,axis=1)

    # the monthly aggregate is compared against the aggregated subscription data
    constraint = numpyro.sample('aggregate',dist.Normal(mean_agg_sub,1e2*np.ones_like(mean_agg_sub)),obs = subscription)

F. Integrate both spending and surveys

class NumPyroIntegratedInference(NumPyroAttribution):
  def __init__(self,spend_data,subscription_data,touch_data,survey_data):
    super(NumPyroIntegratedInference,self).__init__(spend_data,subscription_data,touch_data,survey_data)
  
  def model(self,predict=False):

    if predict:
      spend_data = self.predict_spending
      subscription = self.predict_subscription
      num_channel = self.predict_num_channel
      num_touch = self.predict_num_touch
      num_survey = self.predict_num_survey
      touch_data = self.predict_touch
      survey_data = self.predict_survey
      sample_size = self.predict_sample_size

    else:
      spend_data = self.spending
      subscription = self.subscription
      num_channel = self.num_channel
      num_touch = self.num_touch
      num_survey = self.num_survey
      touch_data = self.touch
      survey_data = self.survey
      sample_size = self.sample_size

    sub_touch_coeff = numpyro.sample('sub_touch_coeff',dist.Uniform(np.zeros(num_touch),np.ones(num_touch)))
    sub_survey_coeff = numpyro.sample('sub_survey_coeff',dist.Normal(1e2*np.ones(num_survey),1e2*np.ones(num_survey)))

    with numpyro.plate('plate1',sample_size):
      per_channel_sub_touch = sub_touch_coeff * touch_data
      per_channel_sub_survey = sub_survey_coeff * survey_data
    
    per_channel_sub = np.hstack((per_channel_sub_touch,per_channel_sub_survey))

    test = numpyro.sample('channel',dist.Normal(per_channel_sub,1e1*np.ones_like(per_channel_sub)))
    mean_agg_sub = np.sum(per_channel_sub,axis=1)
    constraint = numpyro.sample('aggregate',dist.Normal(mean_agg_sub,1e2*np.ones_like(mean_agg_sub)),obs = subscription)

G. Model the touchpoints measurement from hypothetical spending

class NumPyroSpendInference(NumPyroAttribution):
  def __init__(self,spend_data,subscription_data,touch_data,survey_data):
    super(NumPyroSpendInference,self).__init__(spend_data,subscription_data,touch_data,survey_data)
  
  def model(self,predict=False):

    if predict:
      spend_data = self.predict_spending
      subscription = self.predict_subscription
      num_channel = self.predict_num_channel
      num_touch = self.predict_num_touch
      num_survey = self.predict_num_survey
      touch_data = self.predict_touch
      survey_data = self.predict_survey
      sample_size = self.predict_sample_size

    else:
      spend_data = self.spending
      subscription = self.subscription
      num_channel = self.num_channel
      num_touch = self.num_touch
      num_survey = self.num_survey
      touch_data = self.touch
      survey_data = self.survey
      sample_size = self.sample_size

    log1p_spend = np.log1p(spend_data)
    spend_coeff = numpyro.sample('spend_coeff',dist.Normal(1e7*np.ones(num_channel),1e6*np.ones(num_channel)))

    with numpyro.plate('plate1',sample_size):
      mean_touch = spend_coeff*log1p_spend
    
    touch_sample = numpyro.sample('touch_sample',dist.Normal(mean_touch,1e6*np.ones_like(mean_touch)),obs=touch_data)